Safety Valves

Contents
Safety Valve Sizing
An in-depth study of the sizing process for a range of applications, including sizing equations for AD Merkblatt, DIN , TRD, ASME, API, BS6759 and others. Covers more complex issues such as two-phase flow and superheat.
Safety Valve Sizing Introduction
A safety valve must always be sized and able to vent any source of steam so that the pressure within the protected apparatus cannot exceed the maximum allowable accumulated pressure (MAAP). This not only means that the valve has to be positioned correctly, but that it is also correctly set. The safety valve must then also be sized correctly, enabling it to pass the required amount of steam at the required pressure under all possible fault conditions.
Once the type of safety valve has been established, along with its set pressure and its position in the system, it is necessary to calculate the required discharge capacity of the valve. Once this is known, the required orifice area and nominal size can be determined using the manufacturer’s specifications.
In order to establish the maximum capacity required, the potential flow through all the relevant branches, upstream of the valve, need to be considered.
In applications where there is more than one possible flow path, the sizing of the safety valve becomes more complicated, as there may be a number of alternative methods of determining its size. Where more than one potential flow path exists, the following alternatives should be considered:
- The safety valve can be sized on the maximum flow experienced in the flow path with the greatest amount of flow.
- The safety valve can be sized to discharge the flow from the combined flow paths.
This choice is determined by the risk of two or more devices failing simultaneously. If there is the slightest chance that this may occur, the valve must be sized to allow the combined flows of the failed devices to be discharged. However, where the risk is negligible, cost advantages may dictate that the valve should only be sized on the highest fault flow. The choice of method ultimately lies with the company responsible for insuring the plant.
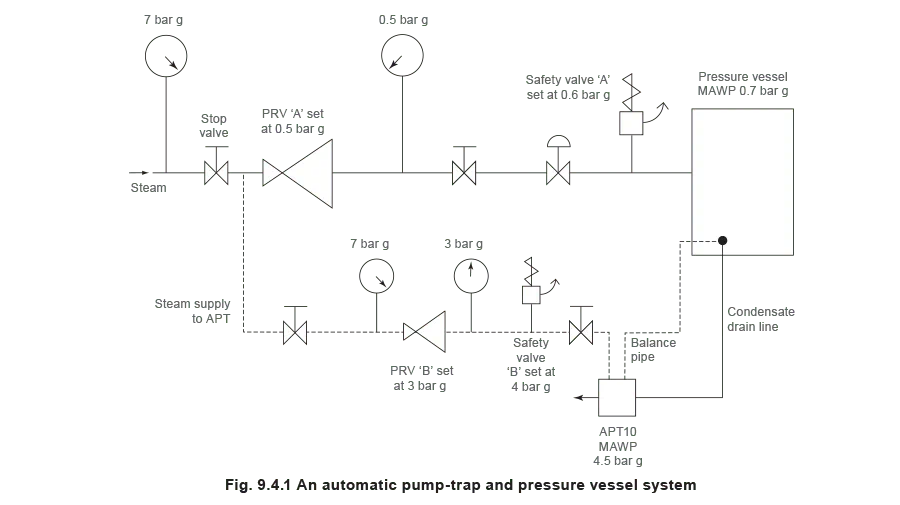
For example, consider the pressure vessel and automatic pump-trap (APT) system as shown in Figure 9.4.1. The unlikely situation is that both the APT and pressure reducing valve (PRV ‘A’) could fail simultaneously. The discharge capacity of safety valve ‘A’ would either be the fault load of the largest PRV, or alternatively, the combined fault load of both the APT and PRV ‘A’.
This document recommends that where multiple flow paths exist, any relevant safety valve should, at all times, be sized on the possibility that relevant upstream pressure control valves may fail simultaneously.
Finding the fault flow
In order to determine the fault flow through a PRV or indeed any valve or orifice, the following need to be considered:
- The potential fault pressure - this should be taken as the set pressure of the appropriate upstream safety valve
- The relieving pressure of the safety valve being sized
- The full open capacity (KVS) of the upstream control valve, see Equation 3.21.2
Example 9.4.1
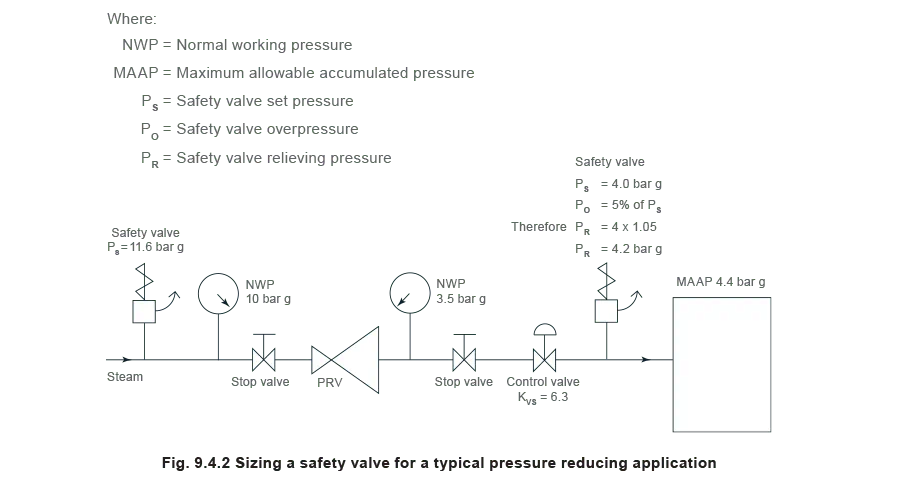
Consider the PRV arrangement in Figure 9.4.2.
The supply pressure of this system (Figure 9.4.2) is limited by an upstream safety valve with a set pressure of 11.6 bar g. The fault flow through the PRV can be determined using the steam mass flow equation (Equation 3.21.2):
In this example:
Consequently, the safety valve would be sized to pass at least 953 kg/h when set at 4 bar g.
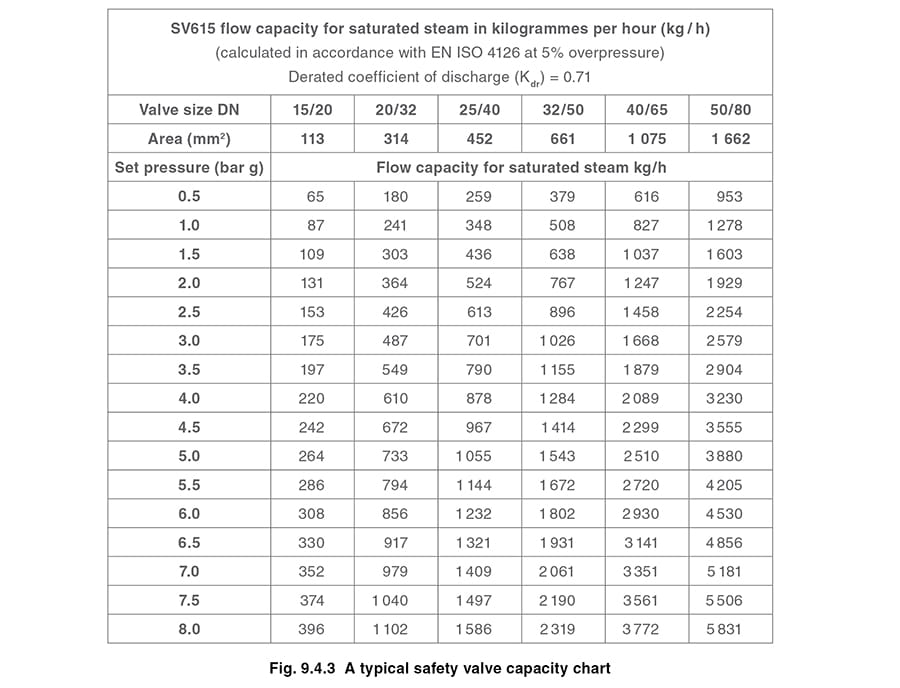
Once the fault load has been determined, it is usually sufficient to size the safety valve using the manufacturer’s capacity charts. A typical example of a capacity chart is shown in Figure 9.4.3. By knowing the required set pressure and discharge capacity, it is possible to select a suitable nominal size. In this example, the set pressure is 4 bar g and the fault flow is 953 kg/h. A DN32/50 safety valve is required with a capacity of 1 284 kg/h.
Where sizing charts are not available or do not cater for particular fluids or conditions, such as backpressure, high viscosity or two-phase flow, it may be necessary to calculate the minimum required orifice area. Methods for doing this are outlined in the appropriate governing standards, such as:
- ASME/API RP 520
- EN ISO 4126
The methods outlined in these standards are based on the coefficient of discharge, which is the ratio of the measured capacity to the theoretical capacity of a nozzle with an equivalent flow area.
Coefficient of discharge
Coefficients of discharge are specific to any particular safety valve range and will be approved by the manufacturer. If the valve is independently approved, it is given a ‘certified coefficient of discharge’.
This figure is often derated by further multiplying it by a safety factor 0.9, to give a derated coefficient of discharge. Derated coefficient of discharge is termed Kdr = Kd x 0.9
When using standard methods of calculating the required orifice area, the following points may need to be considered:
- Critical and sub-critical flow - the flow of gas or vapour through an orifice, such as the flow area of a safety valve, increases as the downstream pressure is decreased. This holds true until the critical pressure is reached, and critical flow is achieved. At this point, any further decrease in the downstream pressure will not result in any further increase in flow. A relationship (called the critical pressure ratio) exists between the critical pressure and the actual relieving pressure, and, for gases flowing through safety valves, is shown by Equation 9.4.2.
For gases, with similar properties to an ideal gas, ‘k’ is the ratio of specific heat of constant pressure (cp) to constant volume (cv), i.e. cp : cv. ‘k’ is always greater than unity, and typically between 1 and 1.4 (see Table 9.4.8).
For steam, although ‘k’ is an isentropic coefficient, it is not actually the ratio of cp : c. As an approximation for saturated steam, ‘k’ can be taken as 1.135, and superheated steam, as 1.3. As a guide, for saturated steam, critical pressure is taken as 58% of accumulated inlet pressure in absolute terms.
- Overpressure - Before sizing, the design overpressure of the valve must be established. It is not permitted to calculate the capacity of the valve at a lower overpressure than that at which the coefficient of discharge was established. It is however, permitted to use a higher overpressure (see Table 9.2.1, Module 9.2, for typical overpressure values). For DIN type full lift (Vollhub) valves, the design lift must be achieved at 5% overpressure, but for sizing purposes, an overpressure value of 10% may be used.
Sizing equations for safety valves designed to the following standards
The following methods are used to calculate the minimum required orifice area for a safety valve, as mentioned in the most commonly used national standards.
Standard - ASME /API RP 520
The following formulae are used for calculating the minimum required orifice area for a safety valve according to ASME standards and the API RP 520 guidelines.
Use Equation 9.4.3 to calculate the minimum required orifice area for a safety valve used on steam applications:

Example 9.4.2
Calculate the minimum required effective discharge area for a safety valve designed to
ASME/API RP520.

Example 9.4.3
Calculate the minimum required effective discharge area for a safety valve designed to ASME/API RP520.

Superheat correction factors for ASME/API RP 520
Table 9.4.1 Superheat correction factors (KSH) as used in ASME/API RP 520 (Imperial units)
| Set pressure (psi g) | Temperature (°F) | |||||||||
| 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1 000 | 1 100 | 1 200 | |
| 15 | 1 | 0.98 | 0.93 | 0.88 | 0.84 | 0.8 | 0.77 | 0.74 | 0.72 | 0.7 |
| 20 | 1 | 0.98 | 0.93 | 0.88 | 0.84 | 0.8 | 0.77 | 0.74 | 0.72 | 0.7 |
| 40 | 1 | 0.99 | 0.93 | 0.88 | 0.84 | 0.81 | 0.77 | 0.74 | 0.72 | 0.7 |
| 60 | 1 | 0.99 | 0.93 | 0.88 | 0.84 | 0.81 | 0.77 | 0.75 | 0.72 | 0.7 |
| 80 | 1 | 0.99 | 0.93 | 0.88 | 0.84 | 0.81 | 0.77 | 0.75 | 0.72 | 0.7 |
| 100 | 1 | 0.99 | 0.94 | 0.89 | 0.84 | 0.81 | 0.77 | 0.75 | 0.72 | 0.7 |
| 120 | 1 | 0.99 | 0.94 | 0.89 | 0.84 | 0.81 | 0.78 | 0.75 | 0.72 | 0.7 |
| 140 | 1 | 0.99 | 0.94 | 0.89 | 0.85 | 0.81 | 0.78 | 0.75 | 0.72 | 0.7 |
| 160 | 1 | 0.99 | 0.94 | 0.89 | 0.85 | 0.81 | 0.78 | 0.75 | 0.72 | 0.7 |
| 180 | 1 | 0.99 | 0.94 | 0.89 | 0.85 | 0.81 | 0.78 | 0.75 | 0.72 | 0.7 |
| 200 | 1 | 0.99 | 0.95 | 0.89 | 0.85 | 0.81 | 0.78 | 0.75 | 0.72 | 0.7 |
| 220 | 1 | 0.99 | 0.95 | 0.89 | 0.85 | 0.81 | 0.78 | 0.75 | 0.72 | 0.7 |
| 240 | 1 | 0.95 | 0.9 | 0.85 | 0.81 | 0.78 | 0.75 | 0.72 | 0.7 | |
| 260 | 1 | 0.95 | 0.9 | 0.85 | 0.81 | 0.78 | 0.75 | 0.72 | 0.7 | |
| 280 | 1 | 0.96 | 0.9 | 0.85 | 0.81 | 0.78 | 0.75 | 0.72 | 0.7 | |
| 300 | 1 | 0.96 | 0.9 | 0.85 | 0.81 | 0.78 | 0.75 | 0.72 | 0.7 | |
| 350 | 1 | 0.96 | 0.9 | 0.86 | 0.82 | 0.78 | 0.75 | 0.72 | 0.7 | |
| 400 | 1 | 0.96 | 0.91 | 0.86 | 0.82 | 0.78 | 0.75 | 0.72 | 0.7 | |
| 500 | 1 | 0.96 | 0.92 | 0.86 | 0.82 | 0.78 | 0.75 | 0.73 | 0.7 | |
| 600 | 1 | 0.97 | 0.92 | 0.87 | 0.82 | 0.79 | 0.75 | 0.73 | 0.7 | |
| 800 | 1 | 0.95 | 0.88 | 0.83 | 0.79 | 0.76 | 0.73 | 0.7 | ||
| 1 000 | 1 | 0.96 | 0.89 | 0.84 | 0.78 | 0.76 | 0.73 | 0.71 | ||
| 1 250 | 1 | 0.97 | 0.91 | 0.85 | 0.8 | 0.77 | 0.74 | 0.71 | ||
| 1 500 | 1 | 1 | 0.93 | 0.86 | 0.81 | 0.77 | 0.74 | 0.71 | ||
Standard - EN ISO 4126: 2004
Use Equation 9.4.4 to calculate the minimum required orifice area for a safety valve used on dry saturated steam (dryness fraction > 0.98) and superheated steam at critical flow:

Use Equation 9.4.5 to calculate the minimum required orifice area for a safety valve used on wet steam applications at critical flow. Note: wet steam must have a dryness fraction greater than 0.9:

Example 9.4.4
Size the minimum flow area required for a safety valve designed to EN ISO 4126 to relieve a superheated steam system of overpressure.

Table 9.4.2
Value of C as a function of ‘k’ for steam, air and gas applications to the EN ISO 4126 standard. The isentropic values, ‘k’ are incorporated into the ISO 4126 standard: (Part 7). Alternatively, ‘k’ values for steam can be obtained from the Spirax Sarco website steam tables.
| k | Cg |
| 0.4 | 1.647 |
| 0.41 | 1.665 |
| 0.42 | 1.682 |
| 0.43 | 1.7 |
| 0.44 | 1.717 |
| 0.45 | 1.733 |
| 0.46 | 1.75 |
| 0.47 | 1.766 |
| 0.48 | 1.782 |
| 0.49 | 1.798 |
| 0.5 | 1.813 |
| 0.51 | 1.829 |
| 0.52 | 1.844 |
| 0.53 | 1.858 |
| 0.54 | 1.873 |
| 0.55 | 1.888 |
| 0.56 | 1.902 |
| 0.57 | 1.916 |
| 0.58 | 1.93 |
| 0.59 | 1.944 |
| 0.6 | 1.957 |
| 0.61 | 1.971 |
| 0.62 | 1.984 |
| 0.63 | 1.997 |
| 0.64 | 2.01 |
| 0.65 | 2.023 |
| 0.66 | 2.035 |
| 0.67 | 2.048 |
| 0.68 | 2.06 |
| 0.69 | 2.072 |
| 0.7 | 2.084 |
| 0.71 | 2.096 |
| 0.72 | 2.108 |
| 0.73 | 2.12 |
| 0.74 | 2.131 |
| 0.75 | 2.143 |
| 0.76 | 2.154 |
| 0.77 | 2.165 |
| 0.78 | 2.17 |
| 0.79 | 2.187 |
| 0.8 | 2.198 |
| 0.81 | 2.209 |
| 0.82 | 2.219 |
| 0.83 | 2.23 |
| 0.84 | 2.24 |
| 0.85 | 2.251 |
| 0.86 | 2.261 |
| 0.87 | 2.271 |
| 0.88 | 2.281 |
| 0.89 | 2.291 |
| 0.9 | 2.301 |
| 0.91 | 2.311 |
| 0.92 | 2.32 |
| 0.93 | 2.33 |
| 0.94 | 2.339 |
| 0.95 | 2.349 |
| 0.96 | 2.358 |
| 0.97 | 2.367 |
| 0.98 | 2.376 |
| 0.99 | 2.386 |
| 1 | 2.401 |
| 1.01 | 2.404 |
| 1.02 | 2.412 |
| 1.03 | 2.421 |
| 1.04 | 2.43 |
| 1.05 | 2.439 |
| 1.06 | 2.447 |
| 1.07 | 2.456 |
| 1.08 | 2.464 |
| 1.09 | 2.472 |
| 1.1 | 2.481 |
| 1.11 | 2.489 |
| 1.12 | 2.497 |
| 1.13 | 2.505 |
| 1.14 | 2.513 |
| 1.15 | 2.521 |
| 1.16 | 2.529 |
| 1.17 | 2.537 |
| 1.18 | 2.545 |
| 1.19 | 2.553 |
| 1.2 | 2.56 |
| 1.21 | 2.568 |
| 1.22 | 2.57 |
| 1.23 | 2.583 |
| 1.24 | 2.591 |
| 1.25 | 2.598 |
| 1.26 | 2.605 |
| 1.27 | 2.613 |
| 1.28 | 2.62 |
| 1.29 | 2.627 |
| 1.3 | 2.634 |
| 1.31 | 2.641 |
| 1.32 | 2.649 |
| 1.33 | 2.656 |
| 1.34 | 2.663 |
| 1.35 | 2.669 |
| 1.36 | 2.676 |
| 1.37 | 2.683 |
| 1.38 | 2.69 |
| 1.39 | 2.697 |
| 1.4 | 2.703 |
| 1.41 | 2.71 |
| 1.42 | 2.717 |
| 1.43 | 2.723 |
| 1.44 | 2.73 |
| 1.45 | 2.736 |
| 1.46 | 2.743 |
| 1.47 | 2.749 |
| 1.48 | 2.755 |
| 1.49 | 2.762 |
| 1.5 | 2.768 |
| 1.51 | 2.774 |
| 1.52 | 2.78 |
| 1.53 | 2.786 |
| 1.54 | 2.793 |
| 1.55 | 2.799 |
| 1.56 | 2.805 |
| 1.57 | 2.811 |
| 1.58 | 2.817 |
| 1.59 | 2.823 |
| 1.6 | 2.829 |
| 1.61 | 2.843 |
| 1.62 | 2.84 |
| 1.63 | 2.846 |
| 1.64 | 2.852 |
| 1.65 | 2.858 |
| 1.66 | 2.863 |
| 1.67 | 2.869 |
| 1.68 | 2.874 |
| 1.69 | 2.88 |
| 1.7 | 2.886 |
| 1.71 | 2.891 |
| 1.72 | 2.897 |
| 1.73 | 2.902 |
| 1.74 | 2.908 |
| 1.75 | 2.913 |
| 1.76 | 2.918 |
| 1.77 | 2.924 |
| 1.78 | 2.929 |
| 1.79 | 2.934 |
| 1.8 | 2.94 |
| 1.81 | 2.945 |
| 1.82 | 2.95 |
| 1.83 | 2.955 |
| 1.84 | 2.96 |
| 1.85 | 2.965 |
| 1.86 | 2.971 |
| 1.87 | 2.976 |
| 1.88 | 2.981 |
| 1.89 | 2.986 |
| 1.9 | 2.991 |
| 1.91 | 2.996 |
| 1.92 | 3.001 |
| 1.93 | 3.006 |
| 1.94 | 3.01 |
| 1.95 | 3.015 |
| 1.96 | 3.02 |
| 1.97 | 3.025 |
| 1.98 | 3.03 |
| 1.99 | 3.034 |
| 2 | 3.039 |
| 2.01 | 3.044 |
| 2.02 | 3.049 |
| 2.03 | 3.053 |
| 2.04 | 3.058 |
| 2.05 | 3.063 |
| 2.06 | 3.067 |
| 2.07 | 3.072 |
| 2.08 | 3.076 |
| 2.09 | 3.081 |
| 2.1 | 3.085 |
| 2.11 | 3.09 |
| 2.12 | 3.094 |
| 2.13 | 3.099 |
| 2.14 | 3.103 |
| 2.15 | 3.107 |
| 2.16 | 3.112 |
| 2.17 | 3.116 |
| 2.18 | 3.121 |
| 2.19 | 3.125 |
| 2.2 | 3.129 |